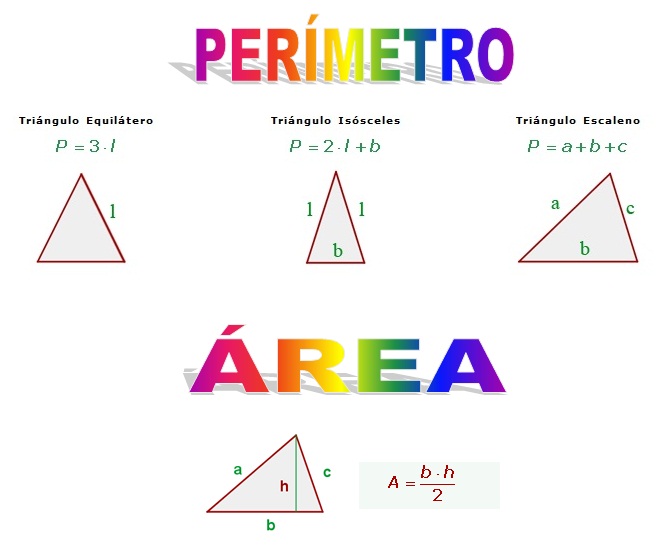
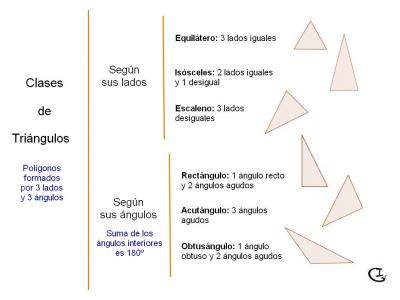
PROBLEMAS DE ÁREA Y PERÍMETRO DE TRIÁNGULOS

1. Determina el perímetro de un triángulo cuya área es 200 m² y su base 25 m, si los lados miden 3 cm más que la altura

 

2. ¿Cuál es la altura de un triángulo que mide 16 cm. de base si su área es equivalente al de un cuadrado de 12 cm. de largo?

 

3. Las bases de un trapecio miden 12 cm. y 21 cm. ¿Cuál es su área si la medida de su altura es igual a la medida de la base menor?

 

4.¿Cuánto mide el lado de un triángulo equilátero cuyo semiperímetro es 2m?

 

5. ¿En cuánto aumenta el área de un triángulo de base 12 m. y 4 m de altura. si se aumentan ambas dimensiones en un 25%?

PERÍMETRO Y ÁREA DE UN TRIÁNGULO

Perímetro de un triángulo

El perímetro de un triángulo es igual a la suma de sus tres lados

Área de un triángulo

El área de un triángulo es igual a base por altura partido por 2.

La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).

 

 

 

TRIÁNGULOS

Triángulo es la figura plana formada por una poligonal cerrada de tres lados, o bien, la figura formada por tres rectas que se cortan, a los puntos de corte se les llama vértices.

Los ángulos del triángulo se designan con letras mayúsculas A,B, y C y los lados opuestos con a, b y c. La suma de los lados es el perímetro y notaremos por p el semiperímetro.

Un ángulo y un lado son adyacentes cuando el vértice del ángulo está sobre el lado, y un lado y un ángulo son opuestos cuando el ángulo no tiene vértice en ese lado.

CLASES DE TRIÁNGULOS:

Según los lados

Equilátero. Los tres lados iguales

Isósceles. Dos lados iguales y el tercero desigual.

Escaleno. Los tres lados desiguales.

Según los ángulos

Rectángulo. Tiene un ángulo recto.

Obtusángulo Tiene un ángulo obtuso.

Acutángulo. Los tres ángulos son agudos.

 

SUMA DE LOS ÁNGULOS INTERNOS DE UN TRIÁNGULO

GEOMETRÍA

La geometría, del griego geo (tierra) y metria (medida), es una rama de la matemática que se ocupa de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, polígonos, poliedros, paralelas, perpendiculares, curvas, superficies, etc. Sus orígenes se remontan a la solución de problemas concretos relativos a medidas y es la justificación teórica de muchos instrumentos, por ejemplo el compás, el teodolito y el pantógrafo. Tiene su aplicación práctica en física, mecánica, cartografía, astronomía, náutica, topografía, balística, etc. También da fundamento teórico a inventos como el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales) y es útil en la preparación de diseños (justificación teórica de la geometría descriptiva, del dibujo técnico e incluso en la fabricación de artesanías).

ACTITUDES HACIA LA MATEMÁTICA

Las actitudes hacia las matemáticas es un tema que ha sido objeto de estudio en diferentes países, niveles escolares, etnias, etc. Uno de los aspectos que más ha llamado la atención de los investigadores ha sido la constatación de que a medida que el estudiante progresa de curso la actitud hacia las matemáticas va siendo más negativa.

El rendimiento académico en matemáticas constituye unos de los desafíos permanentes en la mayoría de los sistemas educativos no sólo porque las matemáticas son consideradas como una de las asignaturas fundamentales en el currículum escolar, sino también por la contribución al desarrollo del conocimiento cognitivo del niño y por la funcionalidad que poseen la mayoría de los aprendizajes matemáticos en la vida adulta. Dada esta importancia, en las sociedades modernas occidentales existe una creciente preocupación por el hecho de que una parte importante de los alumnos, y también la población en general, tiene relevantes dificultades para comprender y utilizar los conocimientos matemáticos.

En los últimos años se ha constatado un aumento de las investigaciones que relacionan la dimensión afectiva del individuo (creencias, actitudes y emociones) y la enseñanza/aprendizaje de las matemáticas. El dominio afectivo está adquiriendo tal protagonismo en este campo que se puede mantener la hipótesis de que las actitudes, las creencias y las emociones influyen tanto en el éxito como en el bajo rendimiento y fracaso en el aprendizaje de las matemáticas.

 

Bienvenido

Ya tienes blog.

Para empezar a publicar artículos y administrar tu nueva bitácora:

1. busca el enlace Administrar en esta misma página.
   
2. Deberás introducir tu clave para poder acceder.

Una vez dentro podrás:

• editar los artículos y comentarios (menú Artículos);
  
• publicar un nuevo texto (Escribir nuevo);
  
• modificar la apariencia y configurar tu bitácora (Opciones);
  
• volver a esta página y ver el blog tal y como lo verían tus visitantes (Salir al blog).

Puedes eliminar este artículo (en Artículos > eliminar). ¡Que lo disfrutes!